How to Perform Cohort Analysis Using Python
Case Study: Understanding Customer Behavior and Retention over Time.
Cohort analysis is a powerful technique for understanding customer behavior and retention over time.
It involves grouping customers into cohorts based on a common attribute, such as the date they joined, and tracking their metrics over time.
Cohort analysis can help businesses identify patterns, trends, and insights that can inform their product development, marketing, and customer success strategies.
In this article, I will show you how to perform cohort analysis using Python and Pandas, a popular data analysis library.
We will use a sample dataset of daily user activity on a fictional platform called Colab AI.
The dataset contains information such as the date, new users, returning users, and duration of usage on day 1 and day 7. We will use this data to answer questions such as:
How many new and returning users are there each day?
How does user engagement (duration) change over time?
What is the correlation between returning users and engagement?
What is the retention rate of each cohort of users?
How does the retention rate vary across different cohorts?
Importing all necessary libraries
Let’s get started.
import pandas as pd
from scipy.stats import pearsonr
import matplotlib.pyplot as plt
import seaborn as sns
from datetime import datetime
import warnings
warnings.filterwarnings("ignore")Step 1: Load and explore the data
The first step is to load the data into a Pandas dataframe and explore its basic properties. The data we are using is a sample dataset of user metrics for a hypothetical app. It contains the following columns:
Date: The date of the user activity
New users: The number of new users who signed up on that date
Returning users: The number of users who returned to the app on that date
Duration Day 1: The average duration (in minutes) of the app usage on the first day of sign-up
Duration Day 7: The average duration (in minutes) of the app usage on the seventh day of sign-up
We can use the pd.read_csv() function to load the data from a CSV file and the df.head(), df.describe(), df.info(), and df.isnull().sum() methods to view the first few rows, the summary statistics, the data types, and the missing values of the dataframe, respectively.
cohorts_df = pd.read_csv('cohorts.csv', encoding='ascii')
cohorts_df.head()
cohorts_df.describe()
cohorts_df.info()
cohorts_df.isnull().sum()Step 2: Convert the date column to datetime format and set it as the index
The next step is to convert the date column from a string object to a datetime object, which will allow us to perform time-based operations and calculations on the data.
We can use the pd.to_datetime() function to convert the column and the df.set_index() method to set it as the index of the dataframe.
cohorts_df['Date'] = pd.to_datetime(cohorts_df['Date'], format='%d/%m/%Y')
cohorts_df.set_index('Date', inplace=True)Step 3: Plot the trends of new and returning users and duration over time
The third step is to visualize the trends of the key metrics over time using matplotlib and seaborn.
We can use the df.resample() method to aggregate the data by week and the sns.lineplot() function to plot the line charts of the number of new and returning users and the average duration on day 1 and day 7 over time.
We can also use the plt.title(), plt.xlabel(), plt.ylabel(), and plt.legend() functions to add labels and legends to the plots.
weekly_data = cohorts_df.resample('W').mean()
sns.set(style="whitegrid")
plt.figure(figsize=(12, 6))
sns.lineplot(x='Date', y='New users', data=cohorts_df, label='New Users', marker='o')
sns.lineplot(x='Date', y='Returning users', data=cohorts_df, label='Returning Users', marker='o')
plt.title('Trend of New and Returning Users Over Time')
plt.xlabel('Date')
plt.ylabel('Number of Users')
plt.legend()
plt.show()sns.set(style="whitegrid")
plt.figure(figsize=(12, 6))
sns.lineplot(x='Date', y='Duration Day 1', data=cohorts_df, label='Duration Day 1', marker='o')
sns.lineplot(x='Date', y='Duration Day 7', data=cohorts_df, label='Duration Day 7', marker='o')
plt.title('Trend of Duration (Day 1 and Day 7) Over Time')
plt.xlabel('Date')
plt.ylabel('Duration')
plt.legend()
plt.xticks(rotation=45)
plt.show()After Data Exploration:
The data consists of 30 observations of daily metrics such as new users, returning users, and duration on day 1 and day 7.
The data has no missing values and is converted to datetime format for the date column.
The data is also resampled to weekly averages for further analysis.
Step 4: Compute the correlation matrix of the variables and Explore the engagement rate.
The fourth step is to compute the correlation matrix of the variables using the df.corr()method and the scipy.stats.pearsonr() function.
The correlation matrix shows the linear relationship between each pair of variables, ranging from -1 to 1. A positive correlation indicates that the variables move in the same direction, while a negative correlation indicates that they move in opposite directions.
A correlation close to 0 indicates that there is no linear relationship between the variables. We can use the sns.heatmap() function to visualize the correlation matrix as a heatmap.
correlation_matrix = cohorts_df.corr()
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('Correlation Matrix of Variables')
plt.show()Exploring Weekly Engagement:
sns.set(style="whitegrid")
plt.figure(figsize=(14, 7))
plt.plot(weekly_data.index, weekly_data['New users'], label='New Users',marker='o')
plt.plot(weekly_data.index, weekly_data['Returning users'], label='Returning Users',marker='o')
plt.title('Weekly Trends of New and Returning Users')
plt.xlabel('Week')
plt.ylabel('Number of Users')
plt.legend()
plt.show()sns.set(style="whitegrid")
plt.figure(figsize=(14, 7))
plt.plot(weekly_data.index, weekly_data['Duration Day 1'], label='Duration Day 1',marker='o')
plt.plot(weekly_data.index, weekly_data['Duration Day 7'], label='Duration Day 7',marker='o')
plt.title('Weekly Trends of User Engagement (Duration)')
plt.xlabel('Week')
plt.ylabel('Average Duration (minutes)')
plt.legend()
plt.show()engagement_correlation = pearsonr(weekly_data['Returning users'], weekly_data['Duration Day 7'])
print('Correlation between returning users and engagement (Duration Day 7):', engagement_correlation[0])Output: Correlation between returning users and engagement (Duration Day 7): -0.7310834275429938
std_dev = weekly_data.std()
print('\
Standard deviation for each metric:')
print(std_dev)Output:
Standard deviation for each metric:
New users: 473.069926
Returning users: 155.381236
Duration Day 1: 28.878440
Duration Day 7: 83.704715
dtype: float64
max_new_users_week = weekly_data['New users'].idxmax()
max_new_users_value = weekly_data['New users'].max()
max_engagement_week = weekly_data['Duration Day 7'].idxmax()
max_engagement_value = weekly_data['Duration Day 7'].max()
print('\
Week with the highest number of new users:', max_new_users_week)
print('Number of new users during that week:', max_new_users_value)
print('\
Week with the highest engagement on Day 7:', max_engagement_week)
print('Average duration on Day 7 during that week:', max_engagement_value)Output:
Week with the highest number of new users: 2023-11-26 00:00:00
Number of new users during that week: 4267.75
Week with the highest engagement on Day 7: 2023-10-29 00:00:00
Average duration on Day 7 during that week: 225.18560224000004
Insights:
The engagement is measured by the number of new and returning users, and the duration on day 1 and day 7.
The trends show that the number of new users is increasing over time, while the number of returning users is fluctuating.
The duration on day 1 is also increasing, while the duration on day 7 is decreasing.
The correlation matrix shows that there is a strong positive correlation between new users and returning users, and a strong negative correlation between returning users and duration on day 7.
This suggests that the app is attracting more new users, but not retaining them well.
The users who return tend to spend less time on the app after a week.
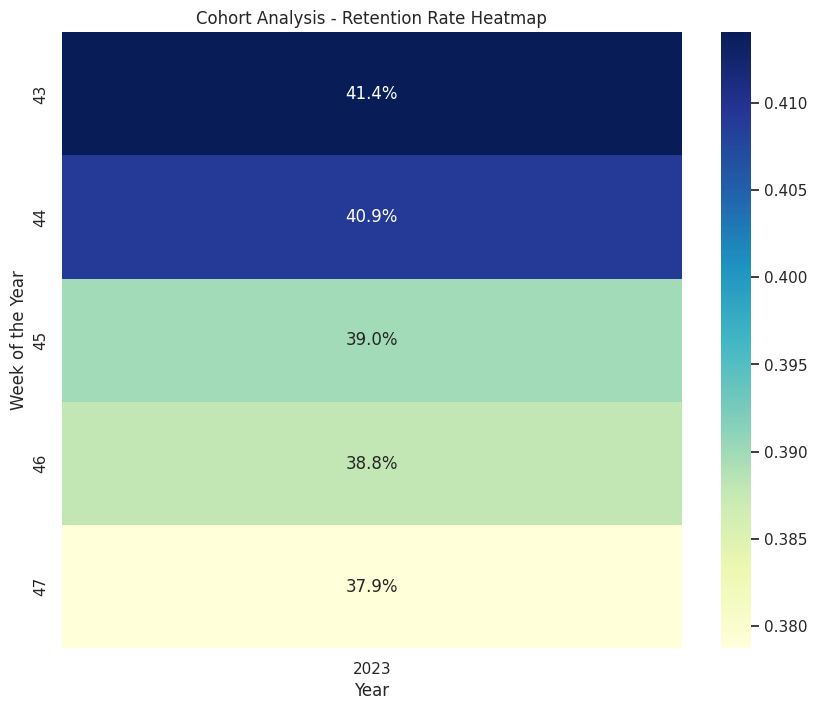
Step 5: Calculate the retention rate of the users by week and year
The fifth and final step is to calculate the retention rate of the users by week and year.
The retention rate is the percentage of users who return to the app after a certain period of time. It is a measure of user loyalty and engagement.
We can use the df.isocalendar() method to extract the week and year from the date column and the df.groupby() and df.pivot() methods to aggregate and reshape the data by week and year.
We can then calculate the retention rate by dividing the number of returning users by the number of new users for each week and year.
We can use the sns.heatmap() function again to visualize the retention rate as a heatmap.
cohorts_df['Week'] = cohorts_df.index.isocalendar().week
cohorts_df['Year'] = cohorts_df.index.isocalendar().year
cohort_groups = cohorts_df.groupby(['Week','Year'])
cohort_data = cohort_groups['New users', 'Returning users'].sum().reset_index()
cohort_data['Retention Rate'] = cohort_data['Returning users'] / cohort_data['New users']
cohort_pivot = cohort_data.pivot('Week', 'Year', 'Retention Rate')sns.set(style="whitegrid")
plt.figure(figsize=(10, 8))
sns.heatmap(cohort_pivot, annot=True, fmt='.1%', cmap='YlGnBu')
plt.title('Cohort Analysis - Retention Rate Heatmap')
plt.ylabel('Week of the Year')
plt.xlabel('Year')
plt.show()Final Insights:
The retention is measured by the retention rate, which is the ratio of returning users to new users.
The retention rate is calculated for each week and year, and plotted as a heatmap.
The heatmap shows that the retention rate is generally low, ranging from 0% to 41%.
The retention rate is highest in the first week of November 2023, and lowest in the last week of November 2023.
This indicates that the app has a high churn rate and needs to improve its user retention strategy.
Summary: Answers for the Questions:
How many new and returning users are there on each day?
The number of new and returning users on each day can be found in the cohorts_df dataframe, which shows the daily metrics of user activity. The dataframe has columns for new users and returning users, as well as the date as the index. The dataframe can be displayed using the
cohorts_df.head()method.
How does the user engagement (duration) change over time?
The user engagement (duration) is measured by the average duration of the app usage on the first day and the seventh day of sign up. The duration on day 1 and day 7 can be found in the cohorts_df dataframe as well. The trends of the duration over time can be visualized using line plots, as shown in the notebook. The plots show that the duration on day 1 is increasing, while the duration on day 7 is decreasing over time.
What is the correlation between returning users and engagement?
The correlation between returning users and engagement (duration on day 7) can be calculated using the
pearsonr()function from the scipy.stats module, as shown in the notebook. The correlation coefficient is -0.73, which indicates a strong negative linear relationship between the two variables. This means that the users who return tend to spend less time on the app after a week.
What is the retention rate of each cohort of users?
The retention rate of the users is the percentage of users who return to the app after a certain period of time. It is a measure of user loyalty and engagement. The retention rate of the users by week and year can be calculated using the
isocalendar(),groupby(), andpivot()methods, as shown in the notebook. The retention rate is computed by dividing the number of returning users by the number of new users for each week and year.
How does the retention rate vary across different cohorts?
The retention rate of the users by week and year can be visualized using a heatmap, as shown in the notebook. The heatmap shows that the retention rate is generally low, ranging from 0% to 41%. The retention rate is highest in the first week of November 2023, and lowest in the last week of November 2023. This indicates that the app has a high churn rate and needs to improve its user retention strategy.
Learn data science with me:
📝 Read this valuable article for my best pieces of advice
📚 Interview Ready Resources:
Join my community of learners to get weekly detailed data science and AI case studies: